TLDR: code is at the end.
It’s well know that we can compute the area of a triangle as the base times the height divided by two.
$$ A = 0.5 \cdot b \cdot h $$
But how do we compute the area given the coordinates of the points?
One efficient way is using the dot product.
We make the vectors $\vec{v_1}$ and $\vec{v_2}$ by linking one point to the other two.
Our $\vec{v_2}$ will be the base of our triangle.
Then we will turn $\vec{v_1}$ 90 degrees ($\vec{v’_1}$).
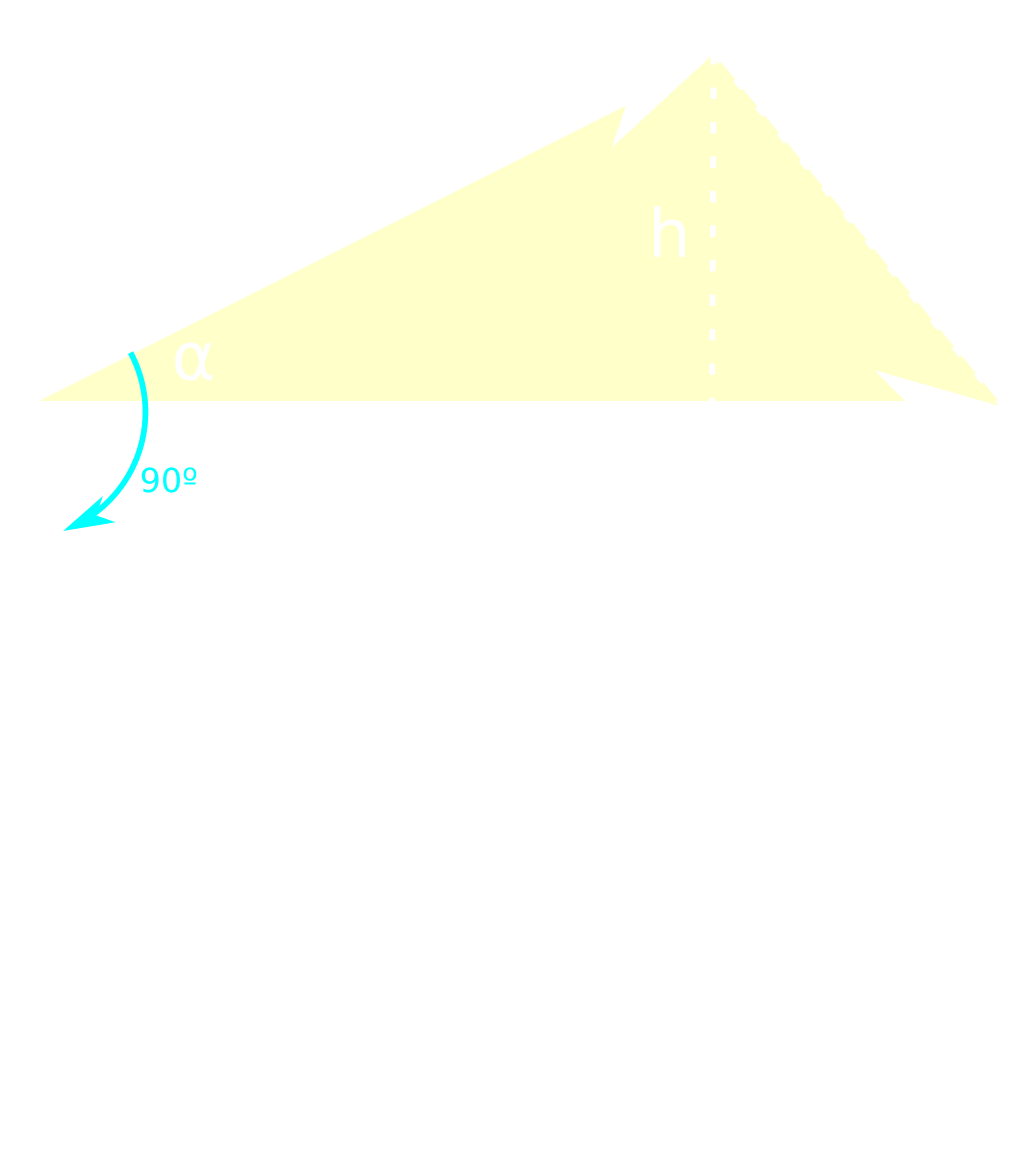
The projection of this rotated $\vec{v^\prime_1}$ on $\vec{v_2}$ is $h$.
That means:
$$ h = cos(\alpha) \lvert \vec{v_2} \rvert = \frac{\vec{v’_1} \cdot \vec{v_2}}{\lvert \vec{v’_1} \rvert} $$
Because of the definition of dot product $\vec{v’_1} \cdot \vec{v_2} = \lvert \vec{v’_1} \rvert \lvert \vec{v_2} \rvert cos(\alpha)$.
Now we can multiply the whole thing by $b$. And we get that.
$$ b \cdot h = \vec{v’_1} \cdot \vec{v_2} $$
$$ A = \frac{b \cdot h}{2} = \frac{\vec{v’_1} \cdot \vec{v_2}}{2} $$
The area you get could be negative! Just take the absolute value.
You can get the same result by using the cross product with 3D vectors (Z = 0).
float triangleArea(vec2 a, vec2 b, vec2 c)
{
const vec2 v1 = b - a;
const vec2 v2 = c - a;
const float dp = v1.y * v2.x - v1.x * v2.y;
return 0.5f * abs(dp);
}